Feature selection (selección de variables)¶

More data beats clever algorithms, but better data beats more data

Definición¶

Proceso manual o automático de identificación de las variables que contribuyen o explican en mayor grado los cambios en la variable dependiente (variable de predicción). Incluir variables irrelevantes afecta negativamente el desempeño de los modelos preditivos porque les inducen a detectar «patrones» basados en aspectos irrelevantes (mayor probabilidad de sobreajuste en los modelos).

Además, eliminar variables innecesarias o redundantes implica otras ventajas:

Simplificación de la descripción de cada observación/ejemplo. Modelos complejos se sobreajustan con mayor facilidad.
Tiempo de entrenamiento menor (hay menos datos que procesar)

Enfoques¶

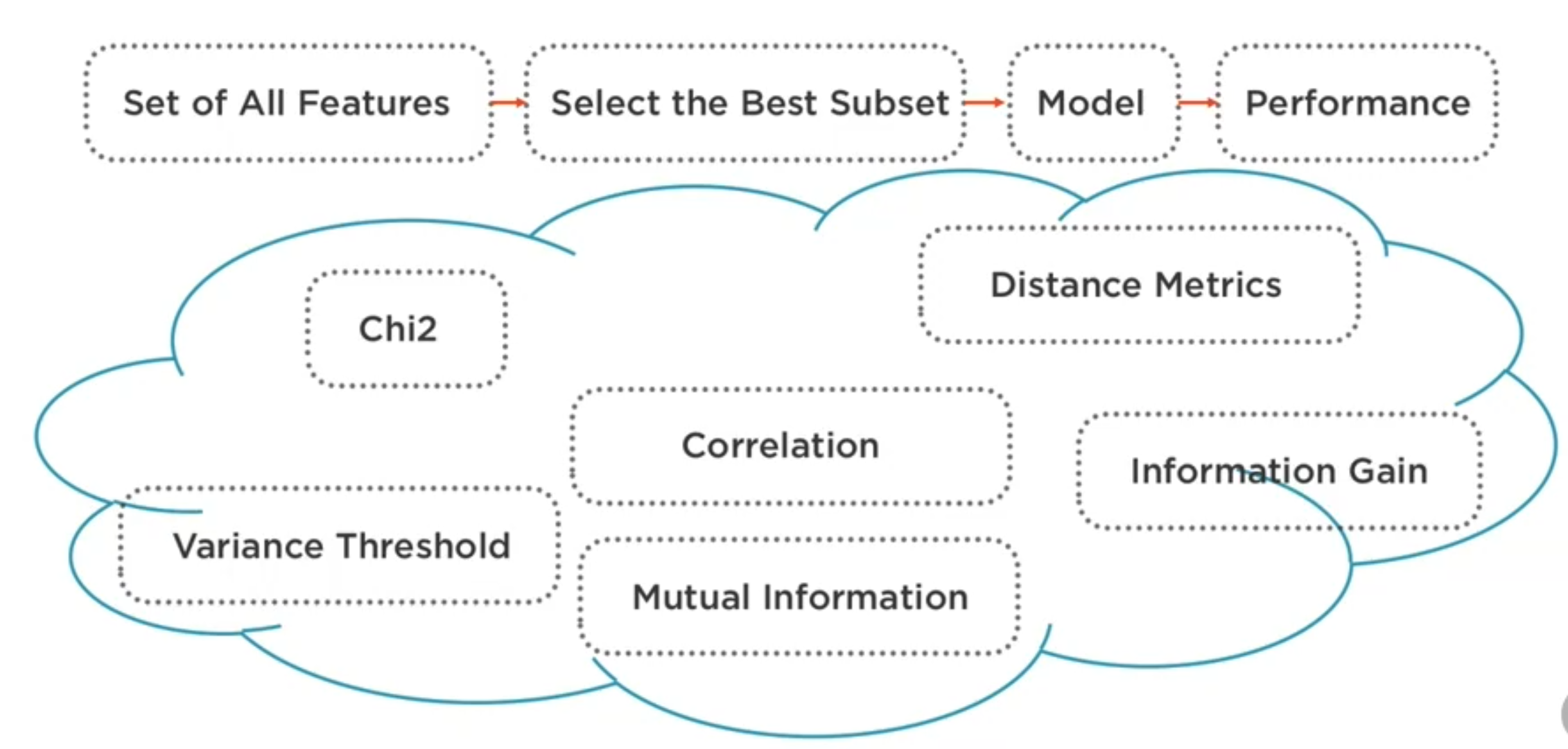
Filtrado a priori (filtering)¶

Estas técnicas buscan eliminar las variables innecesarias antes de emplear los ejemplos/observaciones para entrenar el modelo predictivo.

Estás técnicas son computacionalmente menos costosas que las técnicas wrapper pero no toman en cuenta las caracterísicas del modelo y, por lo tanto, existe la posiblidad de excluir variables que puedan ser útiles. Por lo tanto, se recomienda emplearlas de manera conservadora o evaluar los resultados obtenidos con diferentes conjuntos de variables contra una linea base en la que se emplean todas las variables. Tampoco identifican situaciones de multicolinealidad que pueden tener efectos negativos en modelos de regresión.

Referencias:

../../_images/03-feature-selection-filtering.png

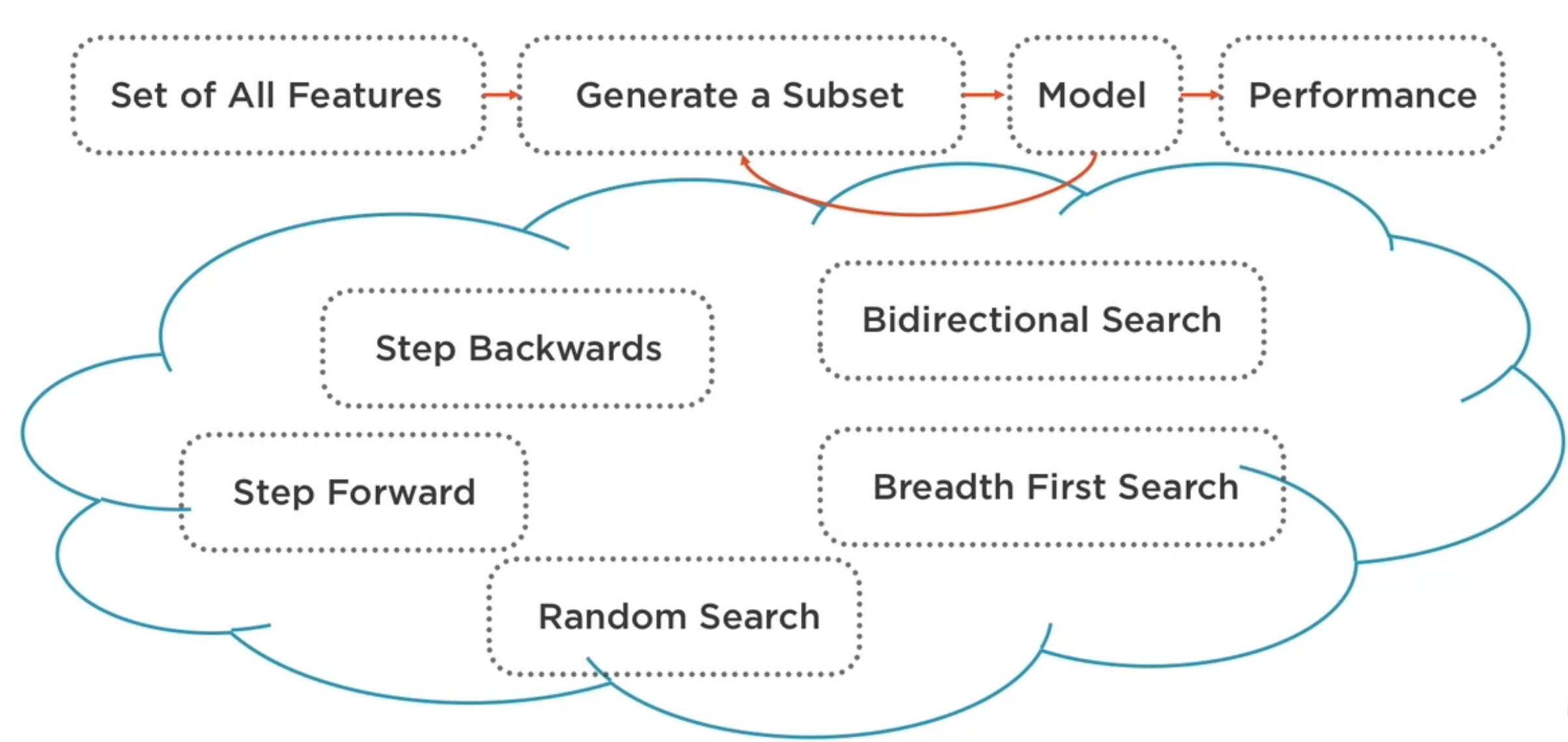
Wrapper¶

Estas técnicas buscan eliminar las variables innecesarias después de emplear los ejemplos/observaciones para entrenar el modelo predictivo y en función de su efecto en el desempeño del mismo. La idea es quedarnos con el subconjunto de las variables que maximizen el desempeño del modelo.

Incrustados (Embedded)¶

Se realiza la selección de las variables como parte del proceso de entrenamiento del modelo. Por ejemplo, en los modelos de clasificación basados en árboles de decisión, el algoritmo que construye el árbol incopora la selección de las variables que clasifican la mayor cantidad de ejemplos.

Técnicas de filtrado a priori¶

Umbral de Varianza (Variance Threshold), para eliminar variables con varianza inferior a un umbral. Mientras más cercana a cero la varianza de una variable, ésta suele ser menos útil para predecir el valor de Y.
Prueba chi cuadrado Para cada variable X, emplear la prueba para determinar si dicha variable y Y son independientes. Si lo son, eliminar X. Si por el contrario, cambios en la variable X provocan cambios significativos en el valor esperado de la variable Y, X se considera signinifiva. Se aplica cuando Y y X son variables categóricas (clasificación)
Información mutua determina la dependencia mutua de dos variables midiendo la reducción de la incertidumbre (entropía) de una variable aleatoria X, debido al conocimiento del valor de otra variable aleatoria Y. Un valor elevado es una indicación de que una variable tiene gran influencia en la otra, cero indica que son independientes. Se considera una técnica superior a ANOVA (Analysis of Variance) por su capacidad capturar relaciones no lineales.

import os
import pandas as pd
import numpy as np
from sklearn.feature_selection import VarianceThreshold

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Input In [1], in <module>
      2 import pandas as pd
      3 import numpy as np
----> 4 from sklearn.feature_selection import VarianceThreshold

ModuleNotFoundError: No module named 'sklearn'

Umbral de Varianza¶

Se puede trabajar también con datos normalizados (z-score)

df = pd.read_csv(os.path.join("boston.csv"))
df.shape

(506, 13)

df.head()

	crime rate	residential land zone	business acres	nitric oxides	number of rooms	age	distances to employment centres	accessibility to highways	property-tax	pupil-teacher ratio	lower income levels	Median Home Value
0	0.00632	18.0	2.31	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	4.98	24.0
1	0.02731	0.0	7.07	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	9.14	21.6
2	0.02729	0.0	7.07	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	4.03	34.7
3	0.03237	0.0	2.18	0.458	6.998	45.8	6.0622	3.0	222.0	18.7	2.94	33.4
4	0.06905	0.0	2.18	0.458	7.147	54.2	6.0622	3.0	222.0	18.7	5.33	36.2

X = df.drop('Median Home Value', axis = 1)
y = df['Median Home Value']
X.head()

	crime rate	residential land zone	business acres	nitric oxides	number of rooms	age	distances to employment centres	accessibility to highways	property-tax	pupil-teacher ratio	lower income levels
0	0.00632	18.0	2.31	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	4.98
1	0.02731	0.0	7.07	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	9.14
2	0.02729	0.0	7.07	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	4.03
3	0.03237	0.0	2.18	0.458	6.998	45.8	6.0622	3.0	222.0	18.7	2.94
4	0.06905	0.0	2.18	0.458	7.147	54.2	6.0622	3.0	222.0	18.7	5.33

X.var(axis = 0)

crime rate                            73.986578
residential land zone                543.936814
business acres                        47.064442
Charles River                          0.064513
nitric oxides                          0.013428
number of rooms                        0.493671
age                                  792.358399
distances to employment centres        4.434015
accessibility to highways             75.816366
property-tax                       28404.759488
pupil-teacher ratio                    4.686989
lower income levels                   50.994760
dtype: float64

X.shape

(506, 12)

#No es muy complicado crear un función equivalente
from sklearn.feature_selection import VarianceThreshold

select_features = VarianceThreshold(threshold = 8.0)

X_new = select_features.fit_transform(X)
X_new

array([[6.3200e-03, 1.8000e+01, 2.3100e+00, ..., 1.0000e+00, 2.9600e+02,
        4.9800e+00],
       [2.7310e-02, 0.0000e+00, 7.0700e+00, ..., 2.0000e+00, 2.4200e+02,
        9.1400e+00],
       [2.7290e-02, 0.0000e+00, 7.0700e+00, ..., 2.0000e+00, 2.4200e+02,
        4.0300e+00],
       ...,
       [6.0760e-02, 0.0000e+00, 1.1930e+01, ..., 1.0000e+00, 2.7300e+02,
        5.6400e+00],
       [1.0959e-01, 0.0000e+00, 1.1930e+01, ..., 1.0000e+00, 2.7300e+02,
        6.4800e+00],
       [4.7410e-02, 0.0000e+00, 1.1930e+01, ..., 1.0000e+00, 2.7300e+02,
        7.8800e+00]])

X_new.shape

(506, 7)

X_new = pd.DataFrame(X_new)
X_new.head()

	0	1	2	3	4	5	6
0	0.00632	18.0	2.31	65.2	1.0	296.0	4.98
1	0.02731	0.0	7.07	78.9	2.0	242.0	9.14
2	0.02729	0.0	7.07	61.1	2.0	242.0	4.03
3	0.03237	0.0	2.18	45.8	3.0	222.0	2.94
4	0.06905	0.0	2.18	54.2	3.0	222.0	5.33

selected_features = []

for i in range(len(X_new.columns)):
    for j in range(len(X.columns)):

        if(X_new.iloc[:,i].equals( X.iloc[:,j])):
            selected_features.append(X.columns[j])
            
selected_features

['crime rate',
 'residential land zone',
 'business acres',
 'age',
 'accessibility to highways',
 'property-tax',
 'lower income levels']

rejected_features = set(list(X)) - set(selected_features)
rejected_features

{'Charles River',
 'distances to employment centres',
 'nitric oxides',
 'number of rooms',
 'pupil-teacher ratio'}

X.var(axis = 0)

crime rate                            73.986578
residential land zone                543.936814
business acres                        47.064442
Charles River                          0.064513
nitric oxides                          0.013428
number of rooms                        0.493671
age                                  792.358399
distances to employment centres        4.434015
accessibility to highways             75.816366
property-tax                       28404.759488
pupil-teacher ratio                    4.686989
lower income levels                   50.994760
dtype: float64

X_new.columns = selected_features

X_new.head()

	crime rate	residential land zone	business acres	age	accessibility to highways	property-tax	lower income levels
0	0.00632	18.0	2.31	65.2	1.0	296.0	4.98
1	0.02731	0.0	7.07	78.9	2.0	242.0	9.14
2	0.02729	0.0	7.07	61.1	2.0	242.0	4.03
3	0.03237	0.0	2.18	45.8	3.0	222.0	2.94
4	0.06905	0.0	2.18	54.2	3.0	222.0	5.33

X.head()

	crime rate	residential land zone	business acres	nitric oxides	number of rooms	age	distances to employment centres	accessibility to highways	property-tax	pupil-teacher ratio	lower income levels
0	0.00632	18.0	2.31	0.538	6.575	65.2	4.0900	1.0	296.0	15.3	4.98
1	0.02731	0.0	7.07	0.469	6.421	78.9	4.9671	2.0	242.0	17.8	9.14
2	0.02729	0.0	7.07	0.469	7.185	61.1	4.9671	2.0	242.0	17.8	4.03
3	0.03237	0.0	2.18	0.458	6.998	45.8	6.0622	3.0	222.0	18.7	2.94
4	0.06905	0.0	2.18	0.458	7.147	54.2	6.0622	3.0	222.0	18.7	5.33

Prueba Chi cuadrado¶

df = pd.read_csv(os.path.join("diabetes.csv"))
df.head()

	Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BodyMassIndex	DiabetesPedigreeFunction	Age	Outcome
0	6	148	72	35	0	33.6	0.627	50	1
1	1	85	66	29	0	26.6	0.351	31	0
2	8	183	64	0	0	23.3	0.672	32	1
3	1	89	66	23	94	28.1	0.167	21	0
4	0	137	40	35	168	43.1	2.288	33	1

df.shape

(768, 9)

X = df.drop('Outcome', axis = 1)
y = df['Outcome']

X.shape

(768, 8)

X.dtypes

Pregnancies                   int64
Glucose                       int64
BloodPressure                 int64
SkinThickness                 int64
Insulin                       int64
BodyMassIndex               float64
DiabetesPedigreeFunction    float64
Age                           int64
dtype: object

X = X.astype(np.float64)

#chi2 determina si cada X,y son indepedientes; 'y' debe ser una variable categórica.
#SelectKBest emplea chi2 para probar cada (X,y) y seleccionar las K mejore variables
from sklearn.feature_selection import chi2, SelectKBest

select_features = SelectKBest(chi2, k=3)

X_new = select_features.fit_transform(X, y)

X_new.shape

(768, 3)

X_new = pd.DataFrame(X_new)

X_new.head()

	0	1	2
0	148.0	0.0	50.0
1	85.0	0.0	31.0
2	183.0	0.0	32.0
3	89.0	94.0	21.0
4	137.0	168.0	33.0

X_new.dtypes

  float64
  float64
  float64
dtype: object

selected_features = []

for i in range(len(X_new.columns)):
    for j in range(len(X.columns)):
        
        if(X_new.iloc[:,i].equals(X.iloc[:,j])): #requiere de X = X.astype(np.float64)
            selected_features.append(X.columns[j])
            
selected_features

['Glucose', 'Insulin', 'Age']

rejected_features = set(list(X)) - set(selected_features)

rejected_features

{'BloodPressure',
 'BodyMassIndex',
 'DiabetesPedigreeFunction',
 'Pregnancies',
 'SkinThickness'}

X_new.columns = selected_features
X_new.head()

	Glucose	Insulin	Age
0	148.0	0.0	50.0
1	85.0	0.0	31.0
2	183.0	0.0	32.0
3	89.0	94.0	21.0
4	137.0	168.0	33.0

X.head()

	Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BodyMassIndex	DiabetesPedigreeFunction	Age
0	6.0	148.0	72.0	35.0	0.0	33.6	0.627	50.0
1	1.0	85.0	66.0	29.0	0.0	26.6	0.351	31.0
2	8.0	183.0	64.0	0.0	0.0	23.3	0.672	32.0
3	1.0	89.0	66.0	23.0	94.0	28.1	0.167	21.0
4	0.0	137.0	40.0	35.0	168.0	43.1	2.288	33.0

Información mutua¶

df = pd.read_csv(os.path.join("diabetes.csv"))
df.head()

	Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BodyMassIndex	DiabetesPedigreeFunction	Age	Outcome
0	6	148	72	35	0	33.6	0.627	50	1
1	1	85	66	29	0	26.6	0.351	31	0
2	8	183	64	0	0	23.3	0.672	32	1
3	1	89	66	23	94	28.1	0.167	21	0
4	0	137	40	35	168	43.1	2.288	33	1

X = df.drop('Outcome', axis = 1)
y = df['Outcome']

X = X.astype(np.float64)

mutual_info_classif determina si cada X,y son indepedientes.

Si “y” es una variable numérica contínua se debe usar mutual_info_regression. SelectPercentile emplea mutual_info_classif para probar cada (X,y) y seleccionar las que estén por encima un valor de 100 retiene todas la variables, un valor de 10 retiene aproximadamente la décima parte de las variables

from sklearn.feature_selection import mutual_info_classif, SelectPercentile

select_features = SelectPercentile(mutual_info_classif, percentile = 30)

X_new = select_features.fit_transform(X, y)

X_new.shape

(768, 3)

X_new = pd.DataFrame(X_new)

X_new.head()

	0	1	2
0	148.0	33.6	50.0
1	85.0	26.6	31.0
2	183.0	23.3	32.0
3	89.0	28.1	21.0
4	137.0	43.1	33.0

selected_features = []

for i in range(len(X_new.columns)):
    for j in range(len(X.columns)):
        
        if(X_new.iloc[:,i].equals(X.iloc[:,j])): #requiere de X = X.astype(np.float64)
            selected_features.append(X.columns[j])
            
selected_features

['Glucose', 'BodyMassIndex', 'Age']

rejected_features = set(list(X)) - set(selected_features)

rejected_features

{'BloodPressure',
 'DiabetesPedigreeFunction',
 'Insulin',
 'Pregnancies',
 'SkinThickness'}

X_new.columns = selected_features
X_new.head()

	Glucose	BodyMassIndex	Age
0	148.0	33.6	50.0
1	85.0	26.6	31.0
2	183.0	23.3	32.0
3	89.0	28.1	21.0
4	137.0	43.1	33.0

X.head()

	Pregnancies	Glucose	BloodPressure	SkinThickness	Insulin	BodyMassIndex	DiabetesPedigreeFunction	Age
0	6.0	148.0	72.0	35.0	0.0	33.6	0.627	50.0
1	1.0	85.0	66.0	29.0	0.0	26.6	0.351	31.0
2	8.0	183.0	64.0	0.0	0.0	23.3	0.672	32.0
3	1.0	89.0	66.0	23.0	94.0	28.1	0.167	21.0
4	0.0	137.0	40.0	35.0	168.0	43.1	2.288	33.0

Introducción a la Ciencia de Datos

Feature selection (selección de variables)

Contenido